Standardfehler einfach erklärt

In der Statistik muss der Standardfehler des Mittelwertes vor allem dann berücksichtigt werden, wenn eine Forschung oder Studie nur Stichproben einer Grundgesamtheit als Grundlage nutzt. Der Standardfehler ist ein Maß, mit dem du berechnen kannst, wie weit der Mittelwert der von dir analysierten Stichprobe vom wirklichen Mittelwert in der Grundgesamtheit abweicht. Oft wird der Standardfehler deshalb auch als Stichprobenfehler bezeichnet oder nach dem englischen Terminus „standard error of the mean“ mit der Abkürzung SEM bezeichnet. Wenn du für deine akademische Arbeit mit Stichproben arbeitest, musst du den Standardfehler bei der Auswertung deiner Ergebnisse unbedingt mit einbeziehen. Weitere Informationen findest du in diesem Artikel von Studi-Kompass!

Der Standardfehler des Mittelwerts

Mit dem als Standardfehler bezeichneten Wert kannst du messen, wie weit der Mittelwert, der anhand einer Stichprobe erzielt wurde, vom Mittelwert der Grundgesamtheit abweicht – mit anderen Worten, wie genau die Resultate der von dir gewählten Stichprobe sind. Dabei gilt, dass der Standardfehler sich in dem Maß verkleinert, indem der Stichprobenumfang zunimmt. 

Formel – Standardfehler des Mittelwertes

Der Standardfehler, hier als SF abgekürzt, ist der Quotient, der aus der Standardabweichung der von dir herangezogenen Stichprobe s_x und der Wurzel aus dem Umfang der Stichprobe (n) gebildet wird. Einfacher und genauer ist es, wenn du die Standardabweichung der Grundgesamtheit bereits kennst und sie einfach durch die Wurzel √n teilen musst. Das ist jedoch in vielen Fällen nicht gegeben.

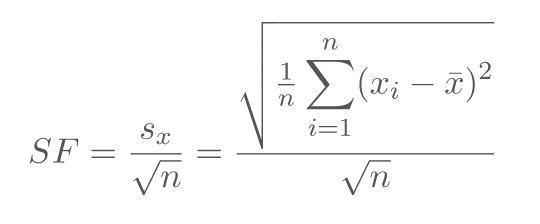
Standardfehler und Standardabweichung

Worin unterscheiden sich nun der Standardfehler und die Standardabweichung? Bei beiden geht es um den Mittelwert, den du auf der Grundlage einer Stichprobe erhoben hast. Der Standardfehler bezeichnet dabei die durchschnittliche Abweichung des Stichproben-Mittelwerts von demjenigen der Grundgesamtheit, der die Stichprobe entnommen wurde.

Die Standardabweichung hingegen gibt Auskunft über die Streuung der Werte aus der Stichprobe um deren Mittelwert. Wenn du aus einer Gruppe von Menschen eines bestimmten Alters immer wieder neue Stichproben von 200 Personen zu ihren Ausgaben für Konsumgüter befragen würdest, kämen dabei unterschiedliche Mittelwerte heraus. Tabellarisch aufgeführt ließe sich dabei für diese Mittelwerte eine bestimmte Anordnung oder Verteilung feststellen. Und aus dieser Streuung könntest du eine Standardabweichung vom Mittelwert und wiederum den Standardfehler ermitteln. 

Berechnung und Interpretation anhand eines anschaulichen Beispiels

Wie schon angedeutet, kannst du dir ein Beispiel vorstellen, bei dem du eine Gruppe von 200 Personen im Alter von 50 Jahren nach ihrem Budget für Konsum befragst. Du wertest die Ergebnisse aus und erhältst dabei einen Stichprobenmittelwert, der dir zeigt, wie viel durchschnittlich in dieser Altersgruppe für Konsumgüter ausgegeben wird. Das wird jedoch kaum ein repräsentatives Ergebnis für die Grundgesamtheit sein, denn die kannst du nur in den seltensten Fällen in einer Stichprobe der Realität entsprechend abbilden.  Wenn du eine zweite Gruppe von 200 Personen im selben Alter befragst, erhältst du zwangsläufig einen abweichenden Stichprobenmittelwert. Der Unterschied beider Mittelwerte lässt sich durch den Standardfehler erfassen. 

Den Standardfehler in Excel berechnen 

Wenn du für deine Abschlussarbeit das Tabellenkalkulationsprogramm Excel nutzt, wirst du schnell merken, dass in Excel keine vordefinierte Formel zur Bestimmung des Standardfehlers enthalten ist. Du kannst die Formel aber ohne weiteres selbst eingeben, so trägst du sie in die Eingabezeile ein: =STDEV(“ ”) /SQRT(count(“ ”)) In die Klammern gehören die Zellen der Tabelle, deren Werte du für die Berechnung des Standardfehlers verwenden willst.