Veröffentlicht am von Carsten Meissner
Der Chi-Quadrat-Test ist ein klassisches Werkzeug der Wissenschaft, um Hypothesen zu prüfen. Er dient dazu, zu prüfen, ob zwei Variablen stochastisch voneinander unabhängig sind. Der Chi-Quadrat-Test ist also in der Lage, zu belegen oder zu widerlegen, ob es einen Zusammenhang zwischen zwei eigentlich unabhängigen Variablen gibt. Betrachten wir den Chi-Quadrat-Test anhand der Beispiele von Studi-Kompass!
Varianten des Chi-Quadrat-Tests
Der Zusammenhang zweier Variablen kann von unterschiedlichen Gesichtspunkten aus betrachtet werden. Der Chi-Quadrat-Test erlaubt es daher, die vorliegenden Hypothesen unterschiedlich zu definieren und entsprechend zu testen. Es gibt drei Grundvarianten für den Chi-Quadrat-Test, welche die Daten jeweils nach einem anderen Aspekt untersuchen.Verteilungstest
Im Rahmen des Verteilungstests wird eine beobachtete Häufigkeit mit einer erwarteten Häufigkeit verglichen.
Beispiel: Unterscheidet sich die Häufigkeit der täglichen Fahrradnutzung von Schulkindern zwischen einer Kleinstadt mit weniger als 20.000 Einwohnern und in ganz Deutschland?
Über den Chi-Quadrat-Verteilungstest lässt sich dann bestimmen, ob Schulkinder in einer Kleinstadt häufiger, weniger häufig oder gleich häufig mit dem Rad unterwegs sind als das durchschnittliche deutsche Schulkind.
Unabhängigkeitstest
Der Unabhängigkeitstest erlaubt es, zwei voneinander unabhängige Variablen in einen Bezug zu setzen.
Beispiel: Nutzen Frauen häufiger öffentliche Verkehrsmittel als Männer?
Hier werden die zwei Variablen des Geschlechts und der Verkehrsmittelnutzung verwendet. Diese haben keinen offensichtlichen Bezug zueinander. Der Chi-Quadrat-Unabhängigkeitstest kann prüfen, ob sie sich dennoch beeinflussen.
Homogenitätstest
Der Homogenitätstest befasst sich mit den Fragen, ob verschiedene Stichproben zu unabhängigen Merkmalen die gleiche Verteilung innerhalb einer Grundgesamtheit aufweisen bzw. ob die gleichen Merkmale aus unterschiedlichen Grundgesamtheiten eine identische Verteilung aufweisen.
Beispiel: Männer und Frauen nutzen mit der gleichen Häufigkeit die öffentlichen Verkehrsmittel.
Hier bildet die Nutzung der öffentlichen Verkehrsmittel das Vergleichsmerkmal und die zwei Grundgesamtheiten sind Männer und Frauen. Die Hypothese in diesem Fall könnte lauten, dass die Verteilung innerhalb der Grundgesamtheiten identisch ist oder dass es einen Unterschied gibt. Die Hypothesenfindung basiert auf den beobachteten Werten.
Voraussetzungen
Um die Berechnungen im Rahmen eines Chi-Quadrat-Tests durchführen zu können, müssen einige Voraussetzungen gegeben sein. So müssen die betrachteten Variablen immer ein nominales oder ordinales Skalaniveau aufweisen. Die Stichprobe sollte mindestens 50 Einheiten umfassen. Darüber hinaus muss sie zufällig genommen werden. Um mit einer Kreuztabelle zu arbeiten, müssen die Daten gruppiert und in absoluten Zahlen vorliegen.
Chi-Quadrat am Beispiel einfach erklärt
Der Test kann in vielen Bereichen zum Einsatz kommen. In diesem Beispiel wird das Chi-Quadrat verwendet, um einen Zusammenhang zwischen dem Einkommen einer Person und dem Schulabschluss einer Person zu betrachten.Hypothese – die Vermutung ist, dass es einen direkten Zusammenhang zwischen dem höchsten Schulabschluss und dem Einkommen einer Person gibt.
- Es werden die Daten von 300 Personen erhoben. Es werden Angaben zum Schulabschluss – Hauptschule, Realschule, Gymnasium – und zum Einkommen gemacht. Das Einkommen wird ebenfalls in drei Kategorien unterteilt.
- Die erhobenen Daten werden zusammen mit den gesamten Kategoriewerten in eine Kreuztabelle eingetragen.
- Diese Daten dienen als Grundlage für die Berechnung, es ist nicht notwendig, weitere Daten für die Berechnung vom Chi-Quadrat zu sammeln oder nachzuschlagen.
Chi-Quadrat berechnen
Umfragedaten in die Kreuztabelle eintragen
| Abschluss/Einkommen |
|
31.000 – 60.000 Euro | 61.000 – 90.000 Euro | |
| Hauptschulabschluss | 39 | 40 | 13 | 92 |
| Realschulabschluss/mittlere Reife | 22 | 48 | 17 | 87 |
| Abitur | 11 | 66 | 44 | 121 |
| 72 | 154 | 74 | 300 |
Die Formel für die Berechnung von Chi-Quadrat sieht so aus:
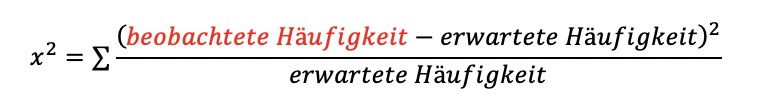
Die beobachteten Häufigkeiten sind bereits in der Tabelle vermerkt. Die erwartete Häufigkeit (fe) muss für jede Zelle nach dieser Formel berechnet werden:

Für den ersten Wert aus der Tabelle lautet die Rechnung also:
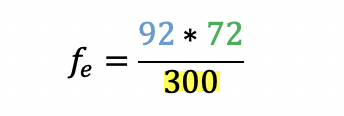
| Abschluss/Einkommen |
|
31.000 – 60.000 Euro | 61.000 – 90.000 Euro | |
| Hauptschulabschluss | 39 / 22,08 | 40 / 47,23 | 13 / 22,70 | 92 |
| Realschulabschluss/mittlere Reife | 22 / 20,88 | 48 / 44,66 | 17 / 21,46 | 87 |
| Abitur | 11 / 29,04 | 66 / 62,11 | 44 / 29,85 | 121 |
| 72 | 154 | 74 | 300 |
Nun sind alle Werte vorhanden, um das Chi-Quadrat für jede Zelle zu berechnen:
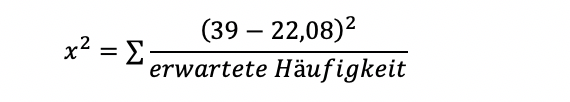
| Abschluss/Einkommen |
|
31.000 – 60.000 Euro | 61.000 – 90.000 Euro | |
| Hauptschulabschluss | 12,97 | 1,11 | 4,15 | 92 |
| Realschulabschluss/mittlere Reife | 0,06 | 0,01 | 0,93 | 87 |
| Abitur | 11,21 | 0,24 | 6,71 | 121 |
| 72 | 154 | 74 | 300 |
Im letzen Rechenschritt werden alle Werte aufsummiert, um den Wert für das Chi-Quadrat zu erhalten.
x2=37,39
Chi-Quadrat-Test interpretieren
Der Wert allein ist nicht aussagekräftig. Die Relevanz des Wertes wird mithilfe des kritischen Wertes bestimmt, der sich aus der Chi-Quadrat-Verteilungstabelle entnehmen lässt. Um diesen Wert abzulesen, müssen das Signifikanzniveau und die sogenannten Freiheitsgrade vorliegen.Das Signifikanzniveau lässt sich frei bestimmen. Allerdings ist es üblich, hier einen Wert von 5% zu nutzen. In der Chi-Quadrat-Verteilungstabelle ist der das Signifikanzniveau α dann mit 0,95 angegeben.
Die Freiheitsgrade für die Signifikanztabelle werden über diese Formel berechnet:
df = (Anzahl der Spalten – 1) * (Anzahl der Zeilen – 1)
Die vorliegende Kreuztabelle hat jeweils drei Einheiten:
df = (3-1) * (3-1) = 4
Der kritische Wert für die vorliegende Berechnung liegt nach der Tabelle bei 9,49.
Übersteigt das berechnete Chi-Quadrat den dazugehörigen kritischen Wert, ist ein Zusammenhang der betrachteten Merkmale anzunehmen. Auf das Beispiel bezogen wurde also rechnerisch nachgewiesen, dass es einen statistisch signifikanten Zusammenhang zwischen dem Einkommen und dem Schulabschluss einer Person gibt. Allerdings ist der Chi-Quadrat-Test nicht in der Lage, rechnerisch zu belegen, in welche Richtung sich der Zusammenhang bewegt und wie stark er ausgeprägt ist.
Chi-Quadrat-Tabelle
Die Chi-Quadrat-Tabelle gibt das Signifikanzniveau α und die Freiheitsgrade an, über welche sich der sogenannte kritische Wert für die Interpretation von x2 bestimmen lässt. Ohne den kritischen Wert lässt sich kein Rückschluss auf den berechneten Wert für das Chi-Quadrat ziehen.
Du hast schon abgestimmt. Danke!

War dieser Artikel hilfreich?

